Skip to contents

Bayesian Supervised Learning in StochTree

Source: vignettes/BayesianSupervisedLearning.Rmd
BayesianSupervisedLearning.Rmd

This vignette demonstrates how to use the bart() function for Bayesian supervised learning (Chipman, George, and McCulloch (2010)). To begin, we load the stochtree package.

Demo 1: Step Function

Simulation

Here, we generate data from a simple step function.

# Generate the data
n <- 500
p_x <- 10
snr <- 3
X <- matrix(runif(n*p_x), ncol = p_x)
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-7.5) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-2.5) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (2.5) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (7.5)
)
noise_sd <- sd(f_XW) / snr
y <- f_XW + rnorm(n, 0, 1)*noise_sd

# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = FALSE))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- as.data.frame(X[test_inds,])
X_train <- as.data.frame(X[train_inds,])
y_test <- y[test_inds]
y_train <- y[train_inds]

Sampling and Analysis

Warmstart

We first sample from an ensemble model of y∣Xy \mid X using “warm-start” initialization samples (He and Hahn (2023)). This is the default in stochtree.

num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_warmstart <- stochtree::bart(
    X_train = X_train, y_train = y_train, X_test = X_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the MCMC samples

plot(bart_model_warmstart$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)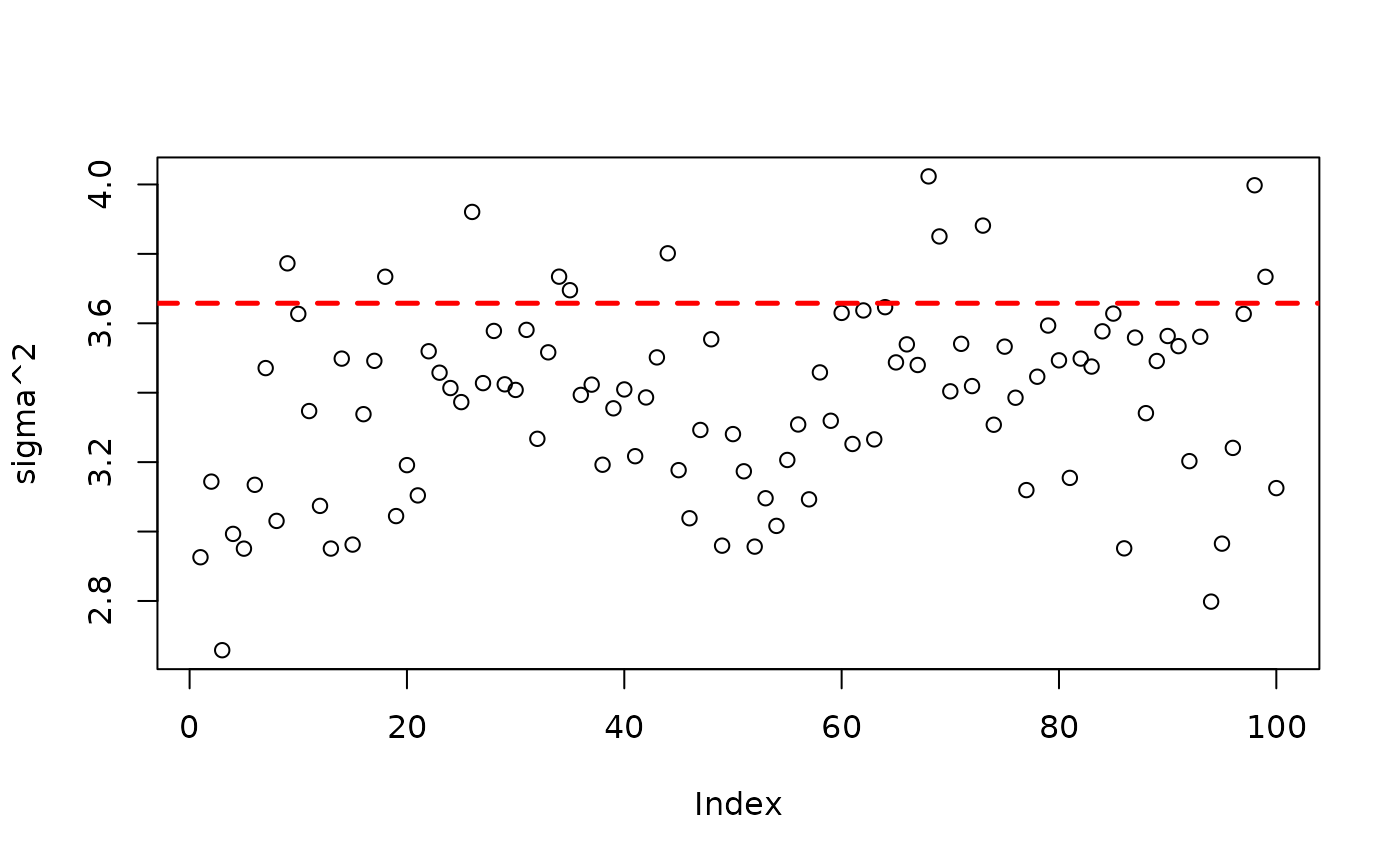

plot(rowMeans(bart_model_warmstart$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)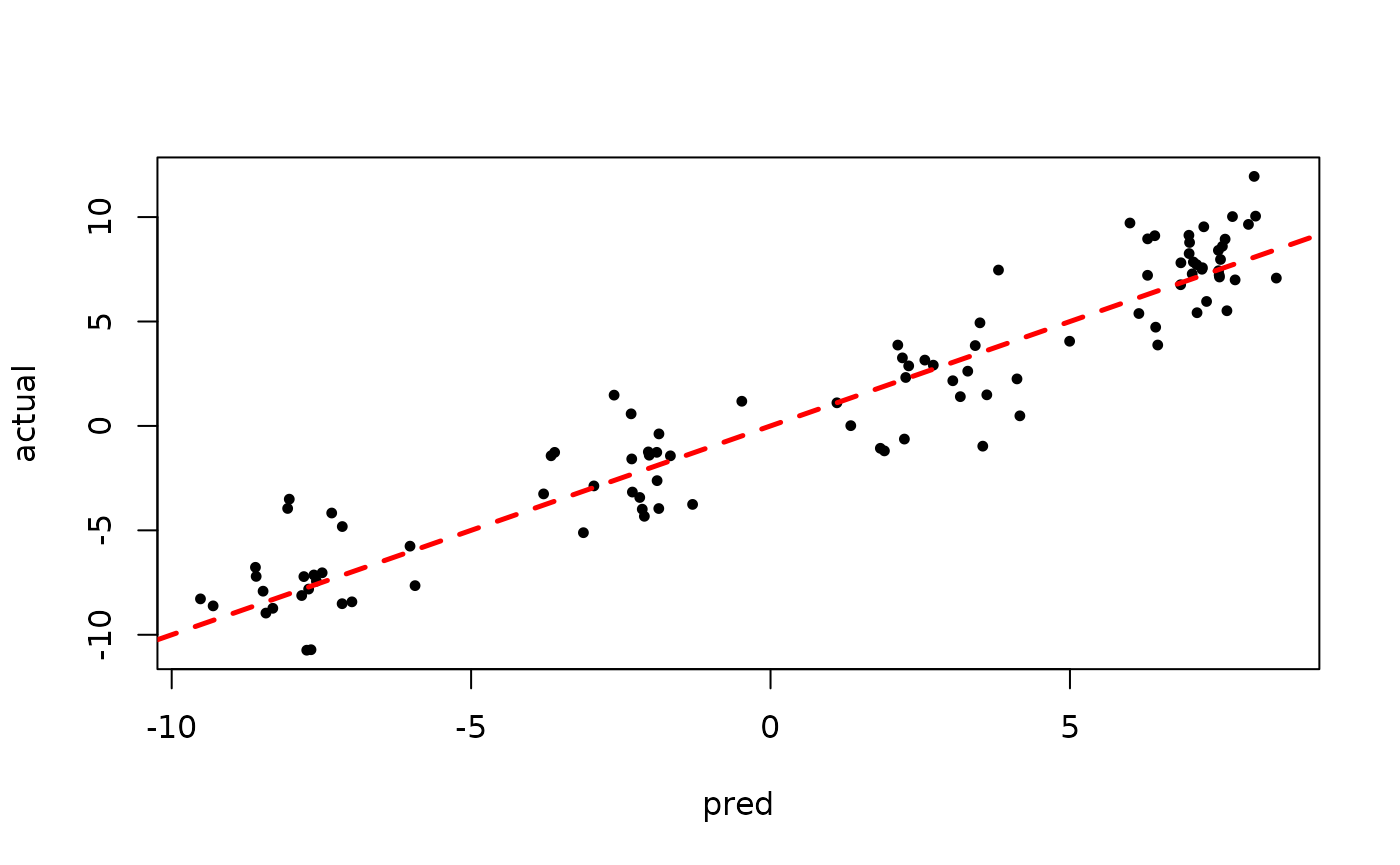

BART MCMC without Warmstart

Next, we sample from this ensemble model without any warm-start initialization.

num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_root <- stochtree::bart(
    X_train = X_train, y_train = y_train, X_test = X_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the MCMC samples

plot(bart_model_root$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)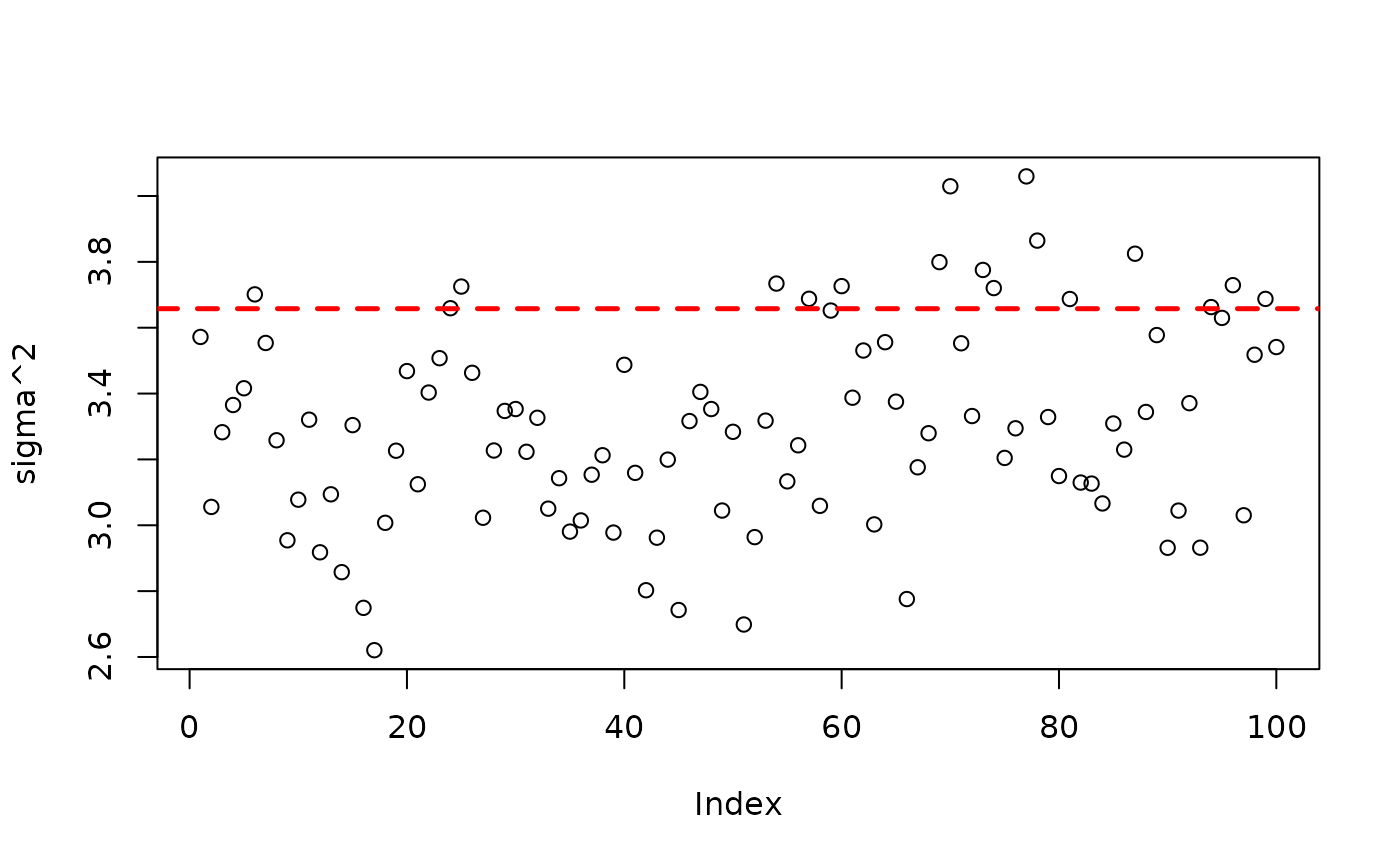

plot(rowMeans(bart_model_root$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)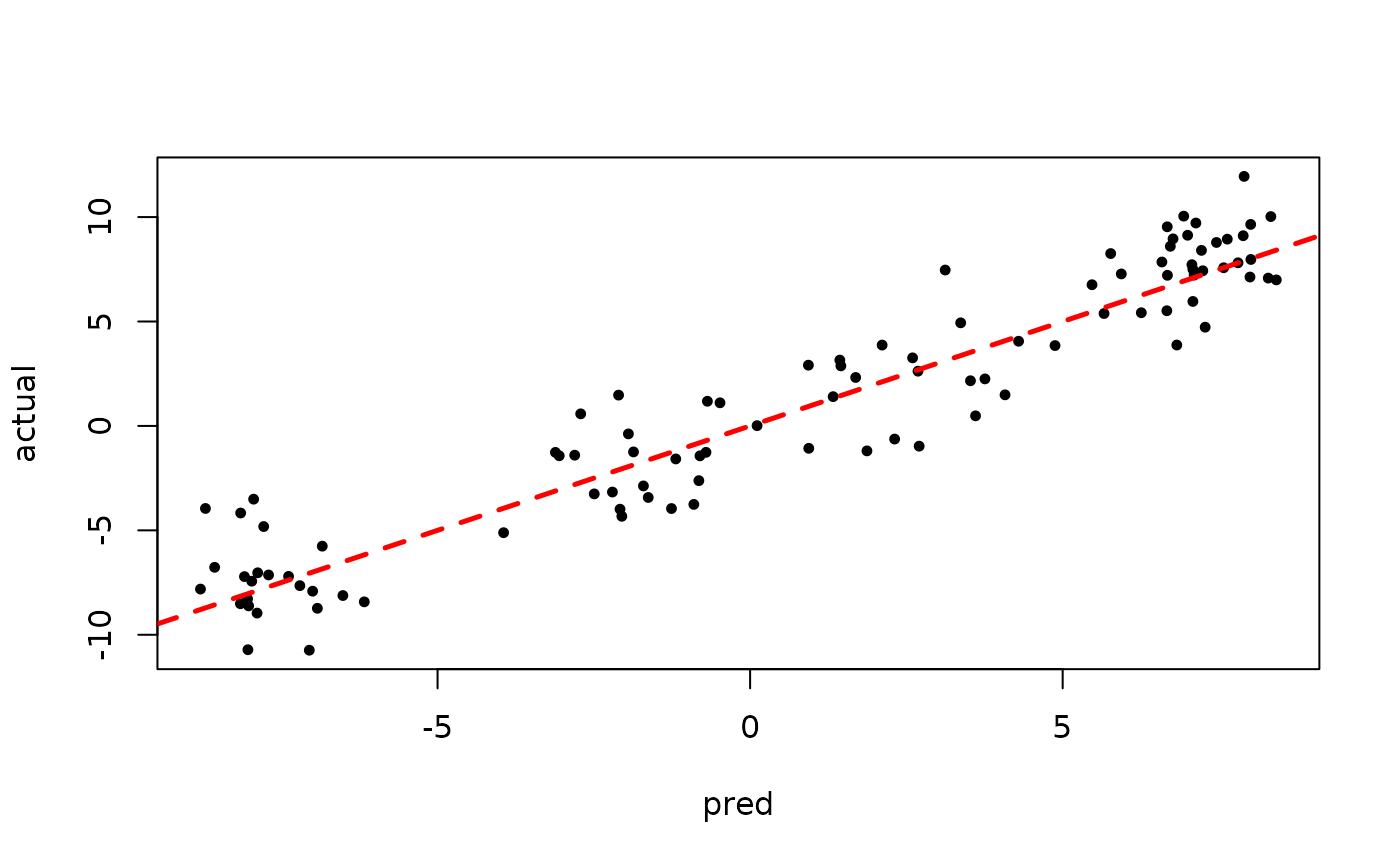

Demo 2: Partitioned Linear Model

Simulation

Here, we generate data from a simple partitioned linear model.

# Generate the data
n <- 500
p_x <- 10
p_w <- 1
snr <- 3
X <- matrix(runif(n*p_x), ncol = p_x)
leaf_basis <- matrix(runif(n*p_w), ncol = p_w)
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-7.5*leaf_basis[,1]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-2.5*leaf_basis[,1]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (2.5*leaf_basis[,1]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (7.5*leaf_basis[,1])
)
noise_sd <- sd(f_XW) / snr
y <- f_XW + rnorm(n, 0, 1)*noise_sd

# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = FALSE))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- as.data.frame(X[test_inds,])
X_train <- as.data.frame(X[train_inds,])
leaf_basis_test <- leaf_basis[test_inds,]
leaf_basis_train <- leaf_basis[train_inds,]
y_test <- y[test_inds]
y_train <- y[train_inds]

Sampling and Analysis

Warmstart

We first sample from an ensemble model of y∣Xy \mid X using “warm-start” initialization samples (He and Hahn (2023)). This is the default in stochtree.

num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_warmstart <- stochtree::bart(
    X_train = X_train, leaf_basis_train = leaf_basis_train, y_train = y_train, 
    X_test = X_test, leaf_basis_test = leaf_basis_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the MCMC samples

plot(bart_model_warmstart$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)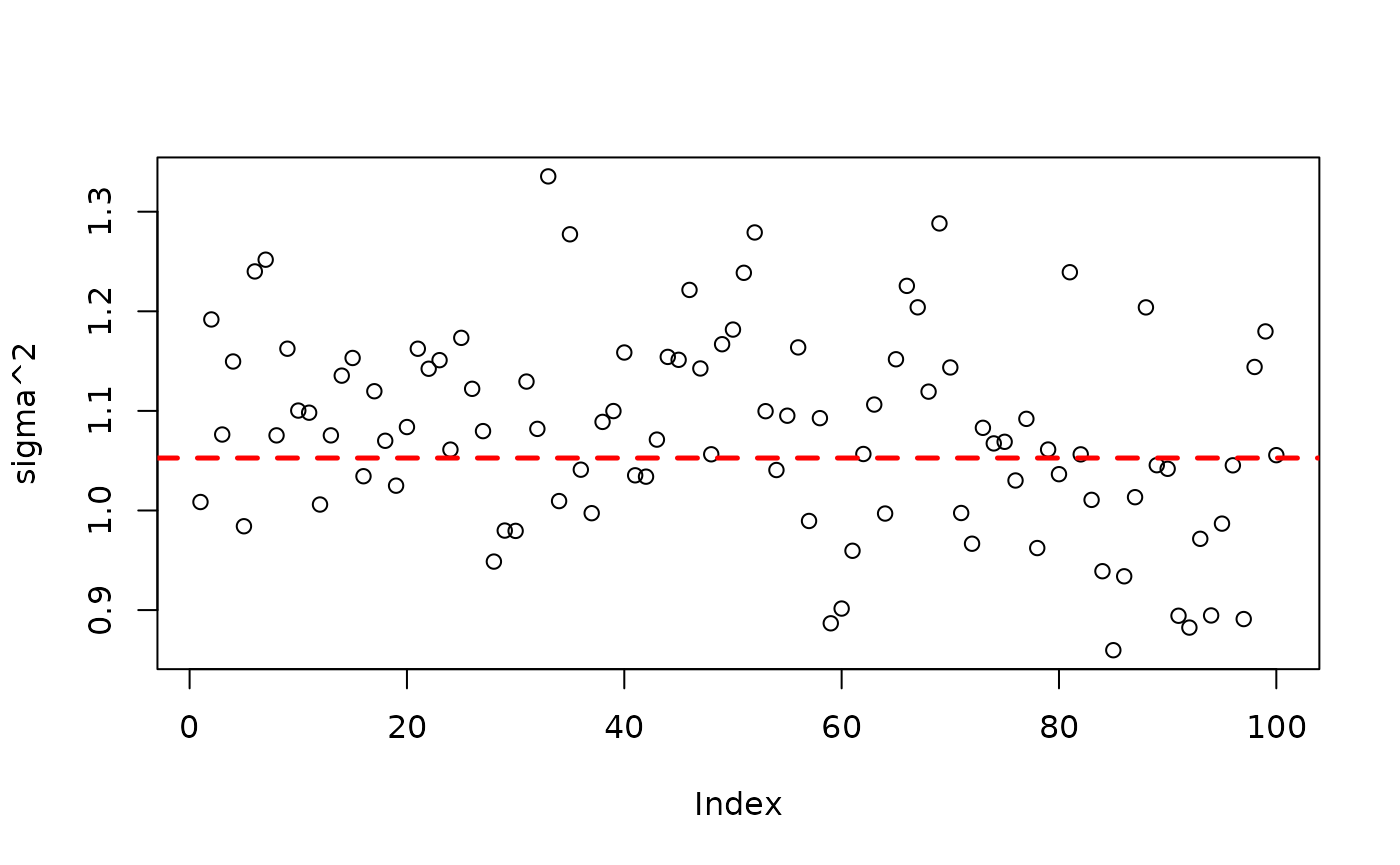

plot(rowMeans(bart_model_warmstart$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)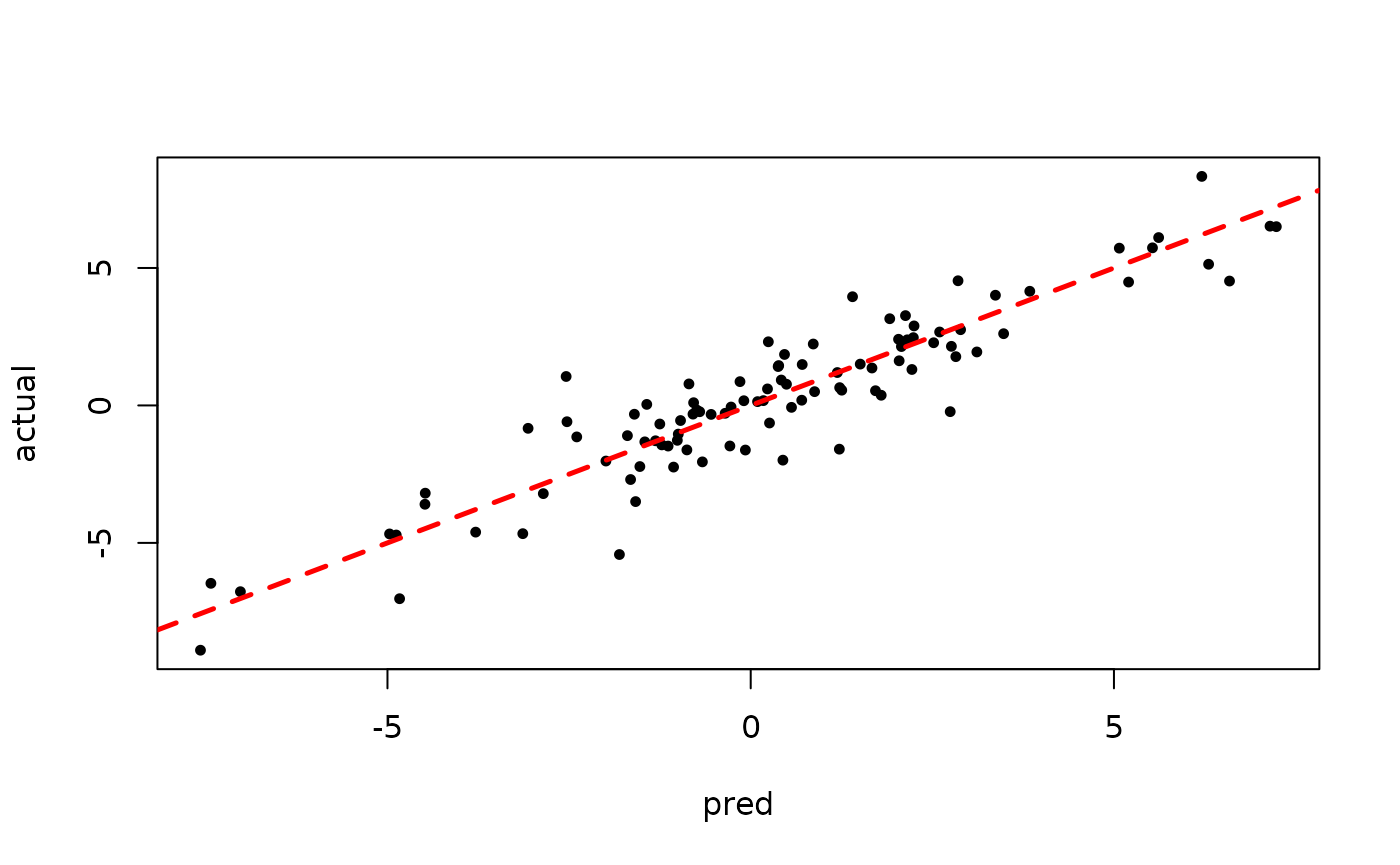

BART MCMC without Warmstart

Next, we sample from this ensemble model without any warm-start initialization.

num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_root <- stochtree::bart(
    X_train = X_train, leaf_basis_train = leaf_basis_train, y_train = y_train, 
    X_test = X_test, leaf_basis_test = leaf_basis_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the BART samples after burnin.

plot(bart_model_root$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)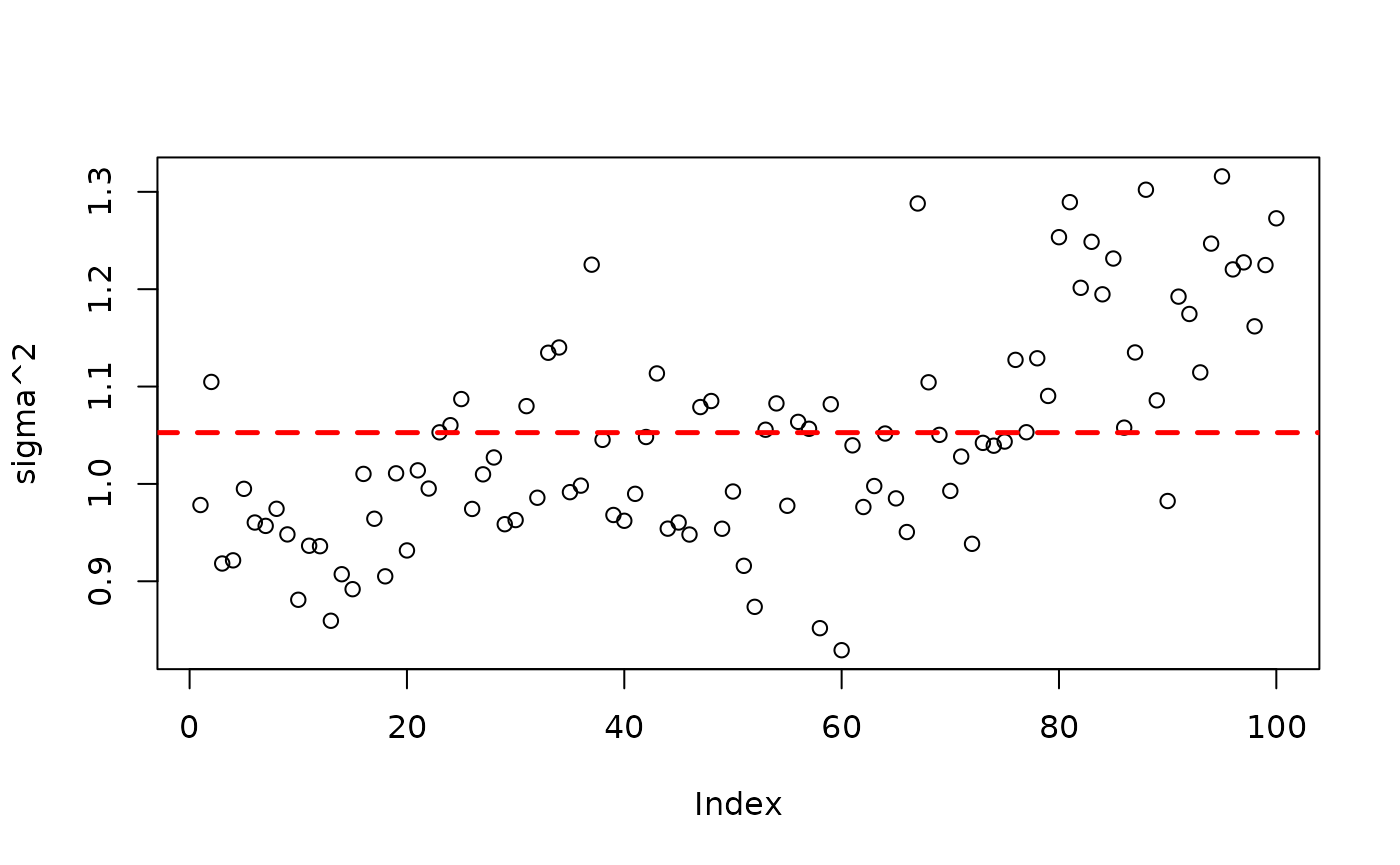

plot(rowMeans(bart_model_root$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)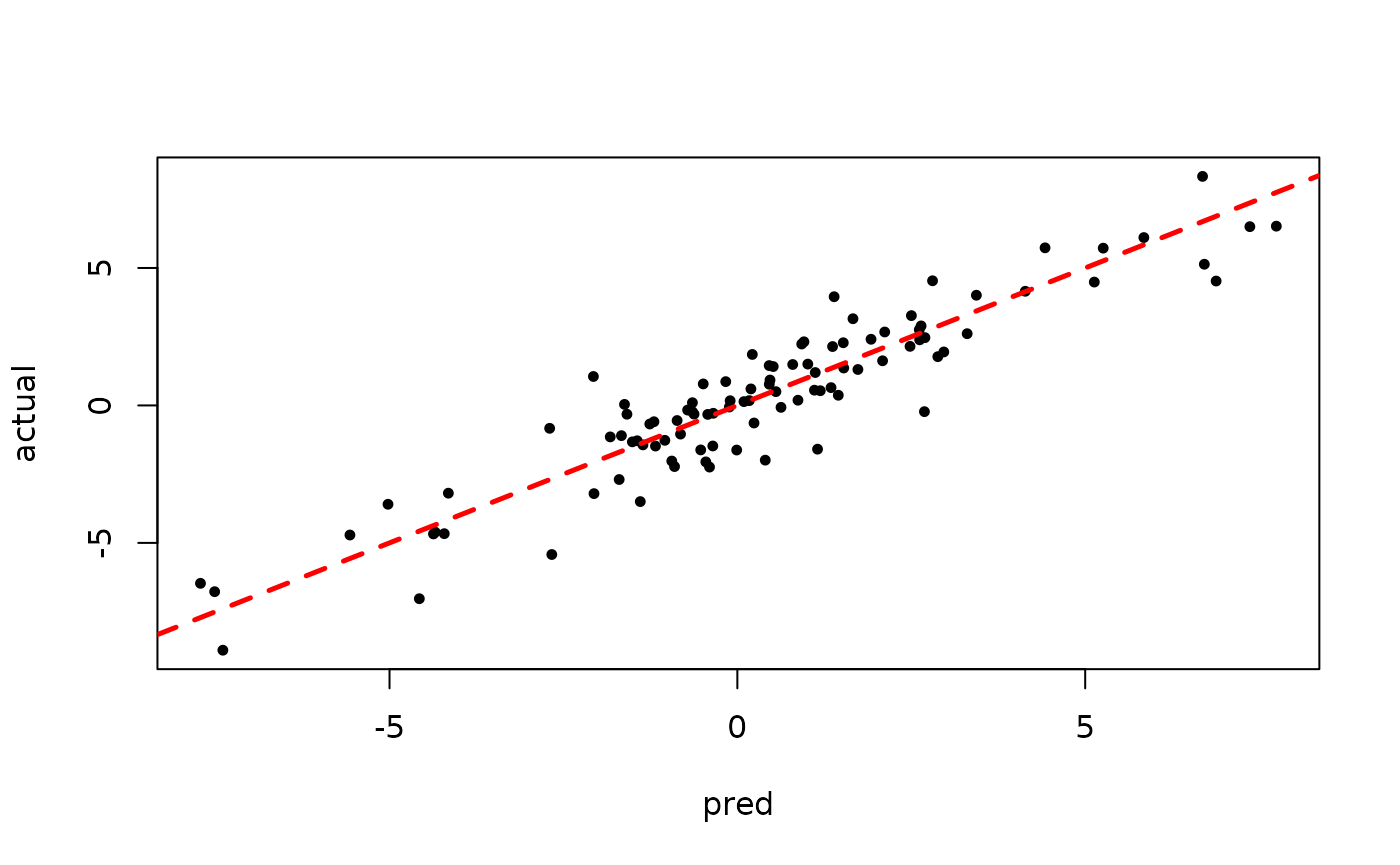

Demo 3: Partitioned Linear Model with Random Effects

Simulation

Here, we generate data from a simple partitioned linear model with an additive random effect structure.

# Generate the data
n <- 500
p_x <- 10
p_w <- 1
snr <- 3
X <- matrix(runif(n*p_x), ncol = p_x)
leaf_basis <- matrix(runif(n*p_w), ncol = p_w)
rfx_group_ids <- rep(c(1,2), n %/% 2)
rfx_coefs <- matrix(c(-5, -3, 5, 3), nrow=2, byrow=TRUE)
rfx_basis <- cbind(1, runif(n, -1, 1))
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-7.5*leaf_basis[,1]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-2.5*leaf_basis[,1]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (2.5*leaf_basis[,1]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (7.5*leaf_basis[,1])
)
rfx_term <- rowSums(rfx_coefs[rfx_group_ids,] * rfx_basis)
noise_sd <- sd(f_XW) / snr
y <- f_XW + rfx_term + rnorm(n, 0, 1)*noise_sd

# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = FALSE))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- as.data.frame(X[test_inds,])
X_train <- as.data.frame(X[train_inds,])
leaf_basis_test <- leaf_basis[test_inds,]
leaf_basis_train <- leaf_basis[train_inds,]
y_test <- y[test_inds]
y_train <- y[train_inds]
rfx_group_ids_test <- rfx_group_ids[test_inds]
rfx_group_ids_train <- rfx_group_ids[train_inds]
rfx_basis_test <- rfx_basis[test_inds,]
rfx_basis_train <- rfx_basis[train_inds,]

Sampling and Analysis

Warmstart

We first sample from an ensemble model of y∣Xy \mid X using “warm-start” initialization samples (He and Hahn (2023)). This is the default in stochtree.

num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_warmstart <- stochtree::bart(
    X_train = X_train, leaf_basis_train = leaf_basis_train, y_train = y_train, rfx_group_ids_train = rfx_group_ids_train, 
    rfx_basis_train = rfx_basis_train, X_test = X_test, leaf_basis_test = leaf_basis_test, rfx_group_ids_test = rfx_group_ids_test,
    rfx_basis_test = rfx_basis_test, num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the MCMC samples

plot(bart_model_warmstart$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)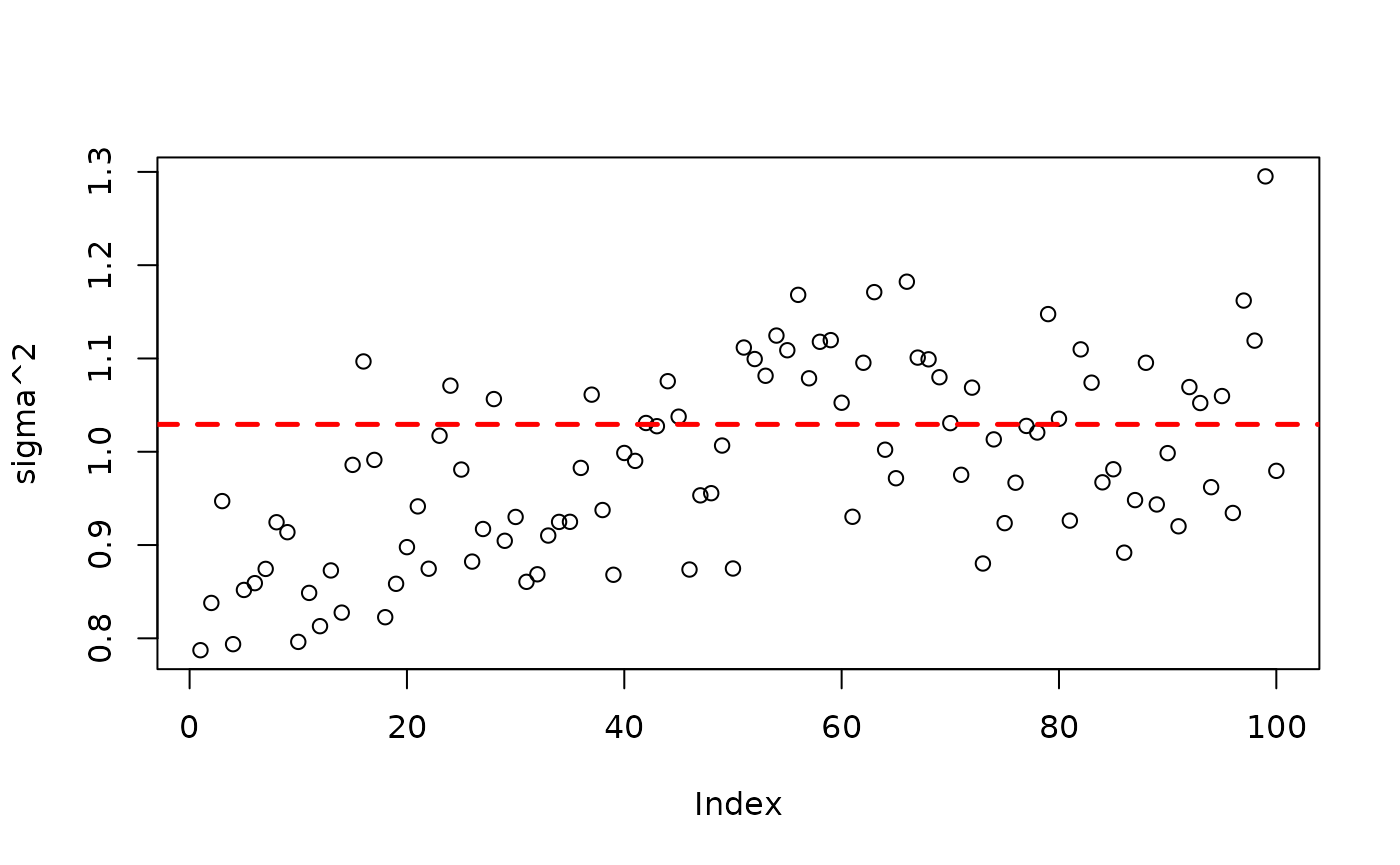

plot(rowMeans(bart_model_warmstart$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)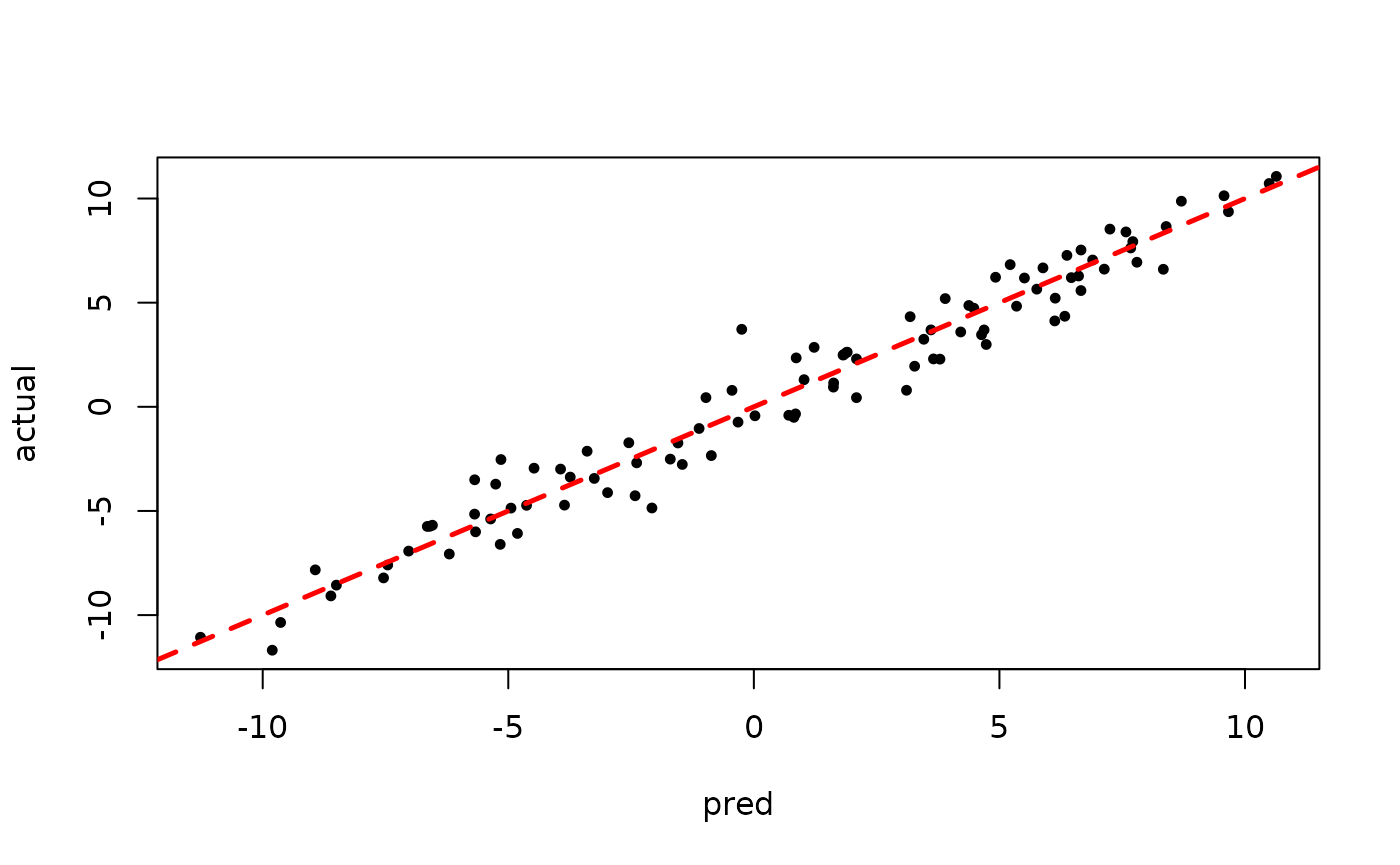

BART MCMC without Warmstart

Next, we sample from this ensemble model without any warm-start initialization.

num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = T)
mean_forest_params <- list(sample_sigma2_leaf = T, num_trees = 100)
bart_model_root <- stochtree::bart(
    X_train = X_train, leaf_basis_train = leaf_basis_train, y_train = y_train, 
    rfx_group_ids_train = rfx_group_ids_train, rfx_basis_train = rfx_basis_train, 
    X_test = X_test, leaf_basis_test = leaf_basis_test, 
    rfx_group_ids_test = rfx_group_ids_test, rfx_basis_test = rfx_basis_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Inspect the MCMC samples

plot(bart_model_root$sigma2_global_samples, ylab="sigma^2")
abline(h=noise_sd^2,col="red",lty=2,lwd=2.5)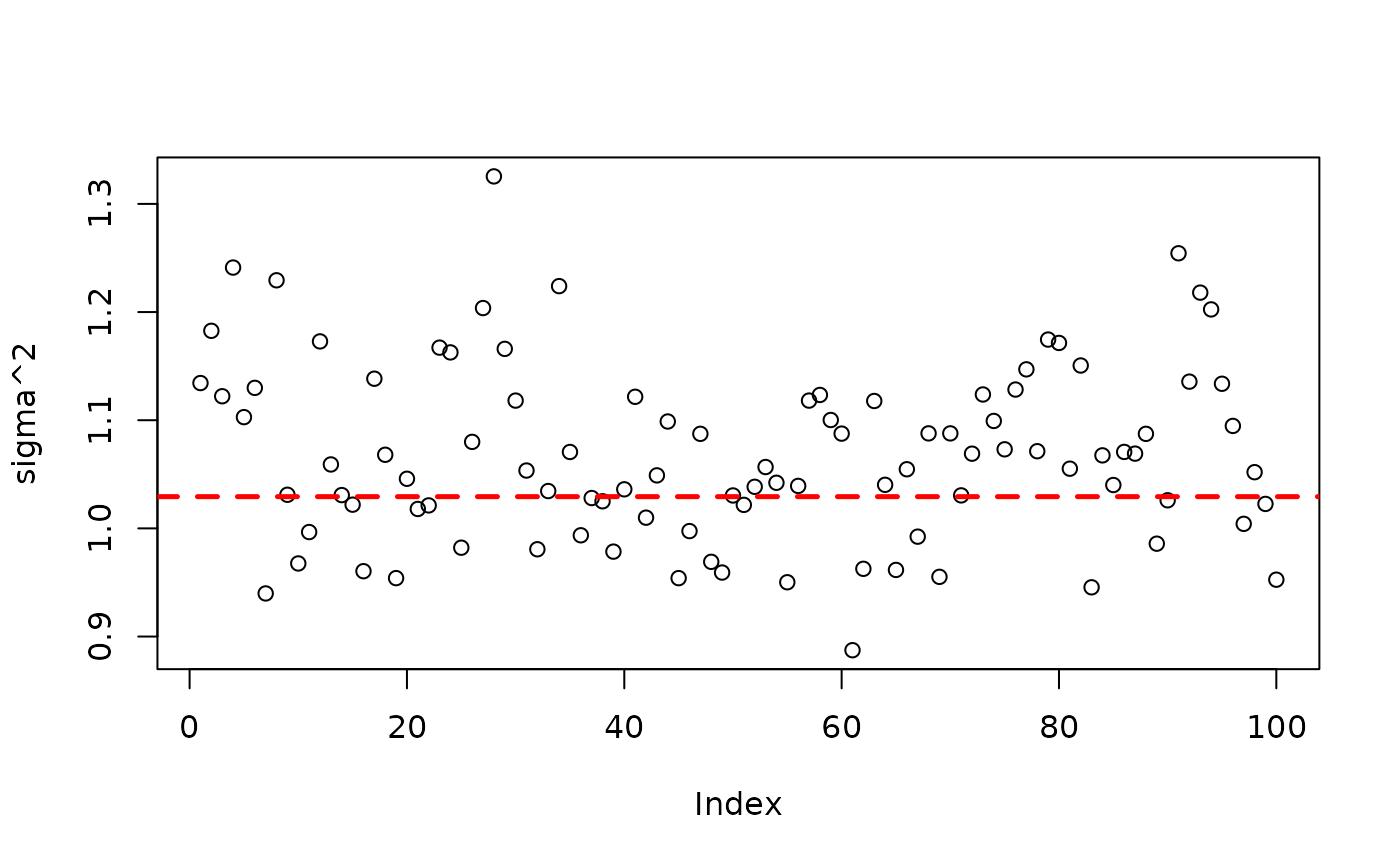

plot(rowMeans(bart_model_root$y_hat_test), y_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)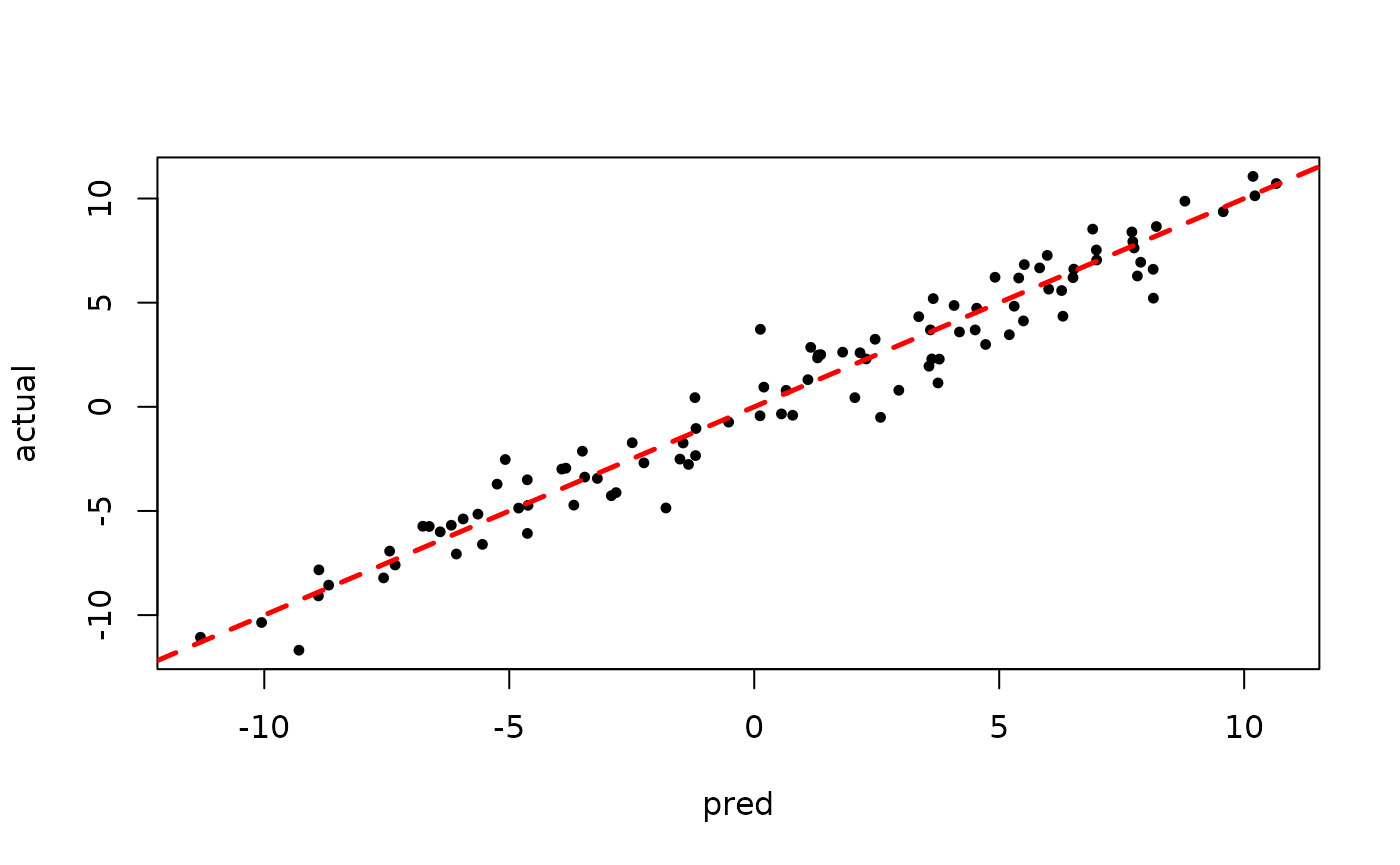

Demo 4: Partitioned Linear Model with Probit Outcome Model

Simulation

Here, we generate data from a simple partitioned linear model.

# Generate the data
n <- 1000
p_x <- 100
X <- matrix(runif(n*p_x), ncol = p_x)
f_X <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-7.5*X[,2]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-2.5*X[,2]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (2.5*X[,2]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (7.5*X[,2])
)
z <- f_X + rnorm(n, 0, 1)
y <- (z>0) * 1.0

# Split data into test and train sets
test_set_pct <- 0.5
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = FALSE))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- as.data.frame(X[test_inds,])
X_train <- as.data.frame(X[train_inds,])
z_test <- z[test_inds]
z_train <- z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]

Sampling and Analysis

Warmstart

We first sample from an ensemble model of y∣Xy \mid X using “warm-start” initialization samples (He and Hahn (2023)). This is the default in stochtree.

num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = F)
mean_forest_params <- list(sample_sigma2_leaf = F, num_trees = 100, 
                           probit_outcome_model = T)
bart_model_warmstart <- stochtree::bart(
    X_train = X_train, y_train = y_train, X_test = X_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Since we’ve simulated this data, we can compare the true latent continuous outcome variable to the probit-scale predictions for a test set.

plot(rowMeans(bart_model_warmstart$y_hat_test), z_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)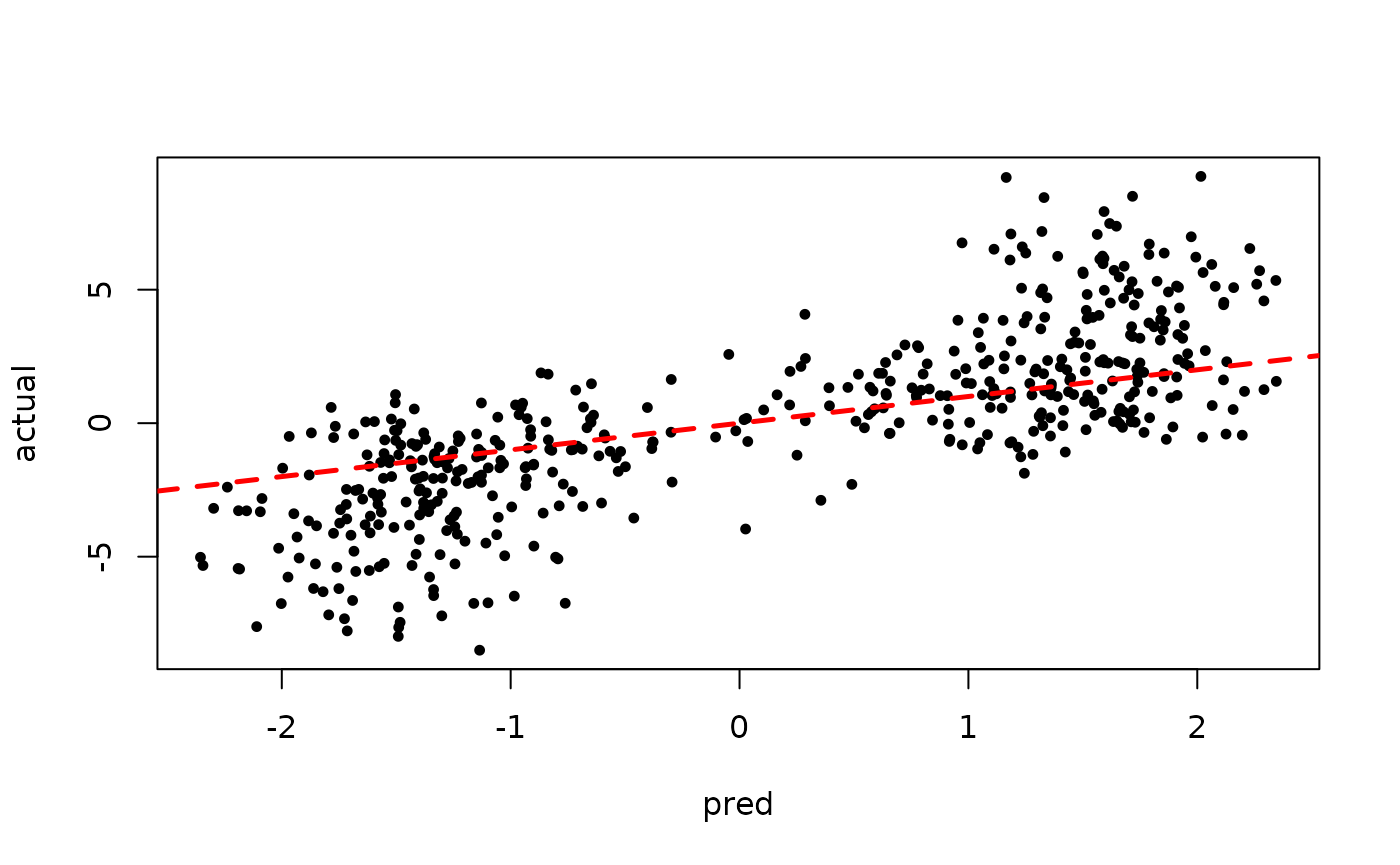

On non-simulated datasets, the first thing we would evaluate is the prediction accuracy.

preds_test <- rowMeans(bart_model_warmstart$y_hat_test) > 0
mean(preds_test == y_test)
#> [1] 0.878

We can also compute the ROC curve for every posterior sample, as well as the ROC of the posterior mean.

num_thresholds <- 1000
thresholds <- seq(0.001,0.999,length.out=num_thresholds)
tpr_mean <- rep(NA, num_thresholds)
fpr_mean <- rep(NA, num_thresholds)
tpr_samples <- matrix(NA, num_thresholds, num_mcmc)
fpr_samples <- matrix(NA, num_thresholds, num_mcmc)
yhat_samples <- bart_model_warmstart$y_hat_test
yhat_mean <- rowMeans(yhat_samples)
for (i in 1:num_thresholds) {
    is_above_threshold_samples <- yhat_samples > qnorm(thresholds[i])
    is_above_threshold_mean <- yhat_mean > qnorm(thresholds[i])
    n_positive <- sum(y_test)
    n_negative <- sum(y_test==0)
    y_above_threshold_mean <- y_test[is_above_threshold_mean]
    tpr_mean[i] <- sum(y_above_threshold_mean)/n_positive
    fpr_mean[i] <- sum(y_above_threshold_mean==0)/n_negative
    for (j in 1:num_mcmc) {
        y_above_threshold <- y_test[is_above_threshold_samples[,j]]
        tpr_samples[i,j] <- sum(y_above_threshold)/n_positive
        fpr_samples[i,j] <- sum(y_above_threshold==0)/n_negative
    }
}

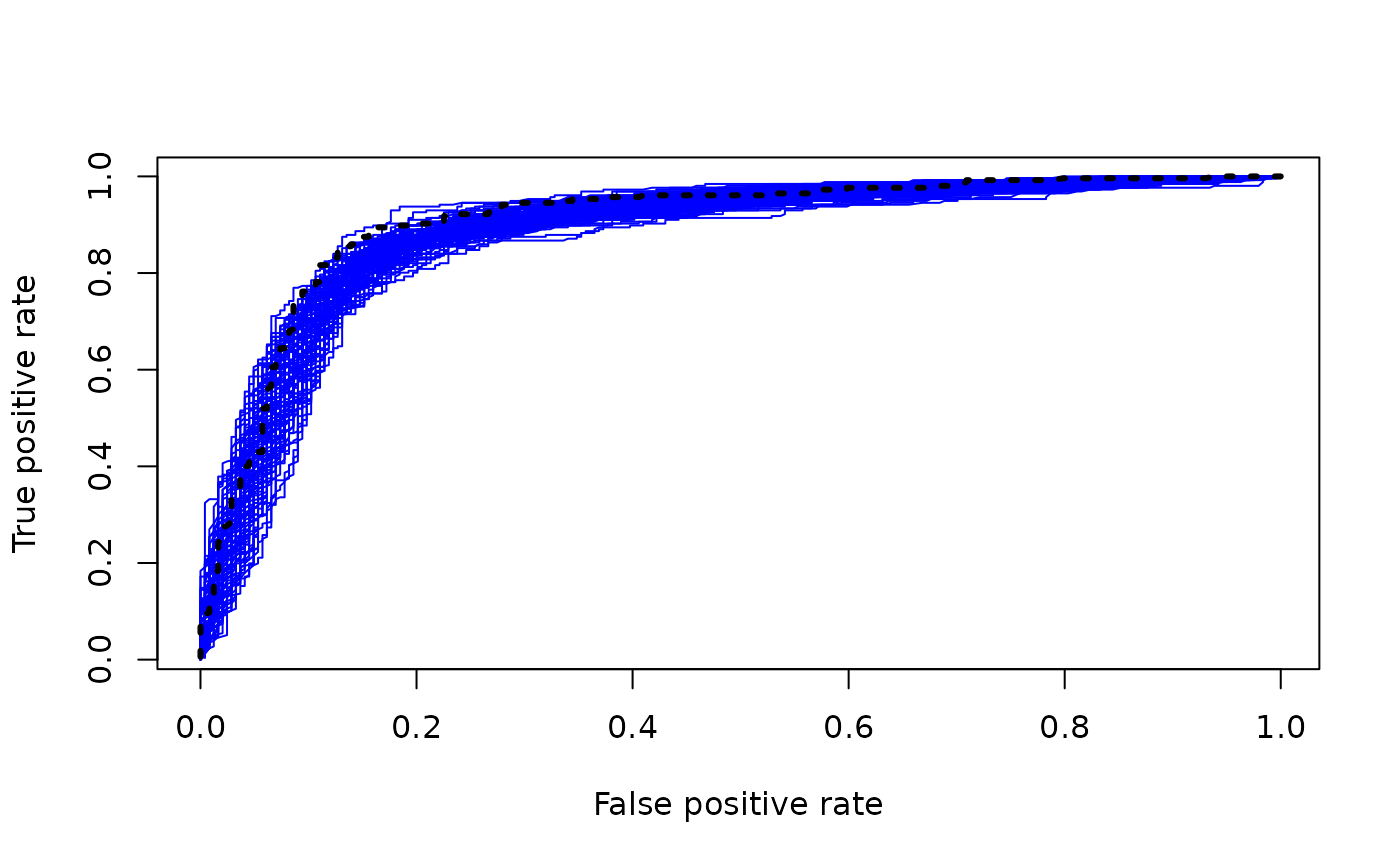
for (i in 1:num_mcmc) {
    if (i == 1) {
        plot(fpr_samples[,i], tpr_samples[,i], type = "line", col = "blue", lwd = 1, lty = 1,
         xlab = "False positive rate", ylab = "True positive rate")
    } else {
        lines(fpr_samples[,i], tpr_samples[,i], col = "blue", lwd = 1, lty = 1)
    }
}
#> Warning in plot.xy(xy, type, ...): plot type 'line' will be truncated to first
#> character
lines(fpr_mean, tpr_mean, col = "black", lwd = 3, lty = 3)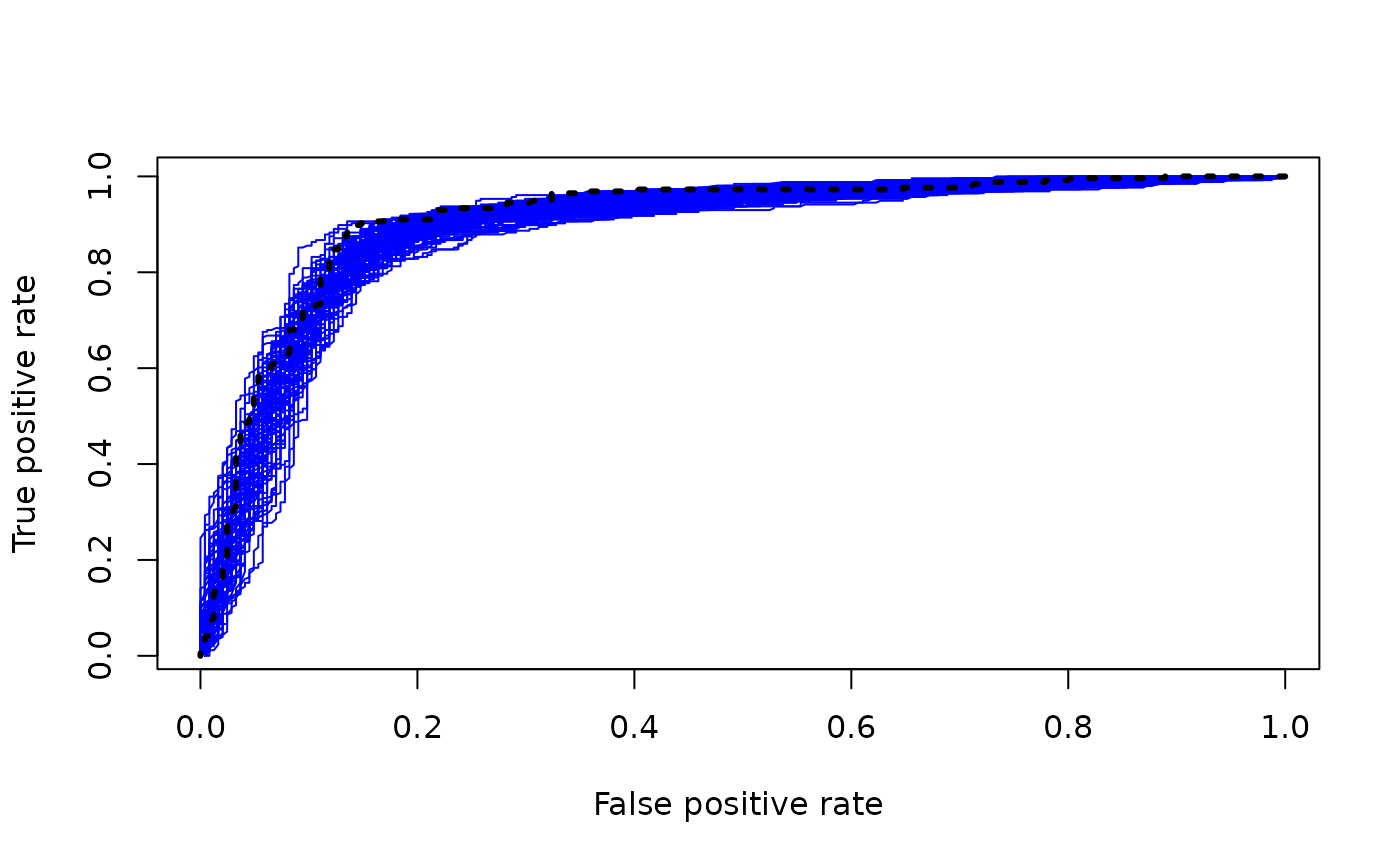

Note that the nonlinearity of the ROC function means that the ROC curve of the posterior mean could sit above most of the individual posterior sample ROC curves (which would not be the case if we had simply taken the mean of the ROC curves).

BART MCMC without Warmstart

Next, we sample from this ensemble model without any warm-start initialization.

num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
general_params <- list(sample_sigma2_global = F)
mean_forest_params <- list(sample_sigma2_leaf = F, num_trees = 100, 
                           probit_outcome_model = T)
bart_model_root <- stochtree::bart(
    X_train = X_train, y_train = y_train, X_test = X_test, 
    num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc, 
    general_params = general_params, mean_forest_params = mean_forest_params
)

Since we’ve simulated this data, we can compare the true latent continuous outcome variable to the probit-scale predictions for a test set.

plot(rowMeans(bart_model_root$y_hat_test), z_test, 
     pch=16, cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)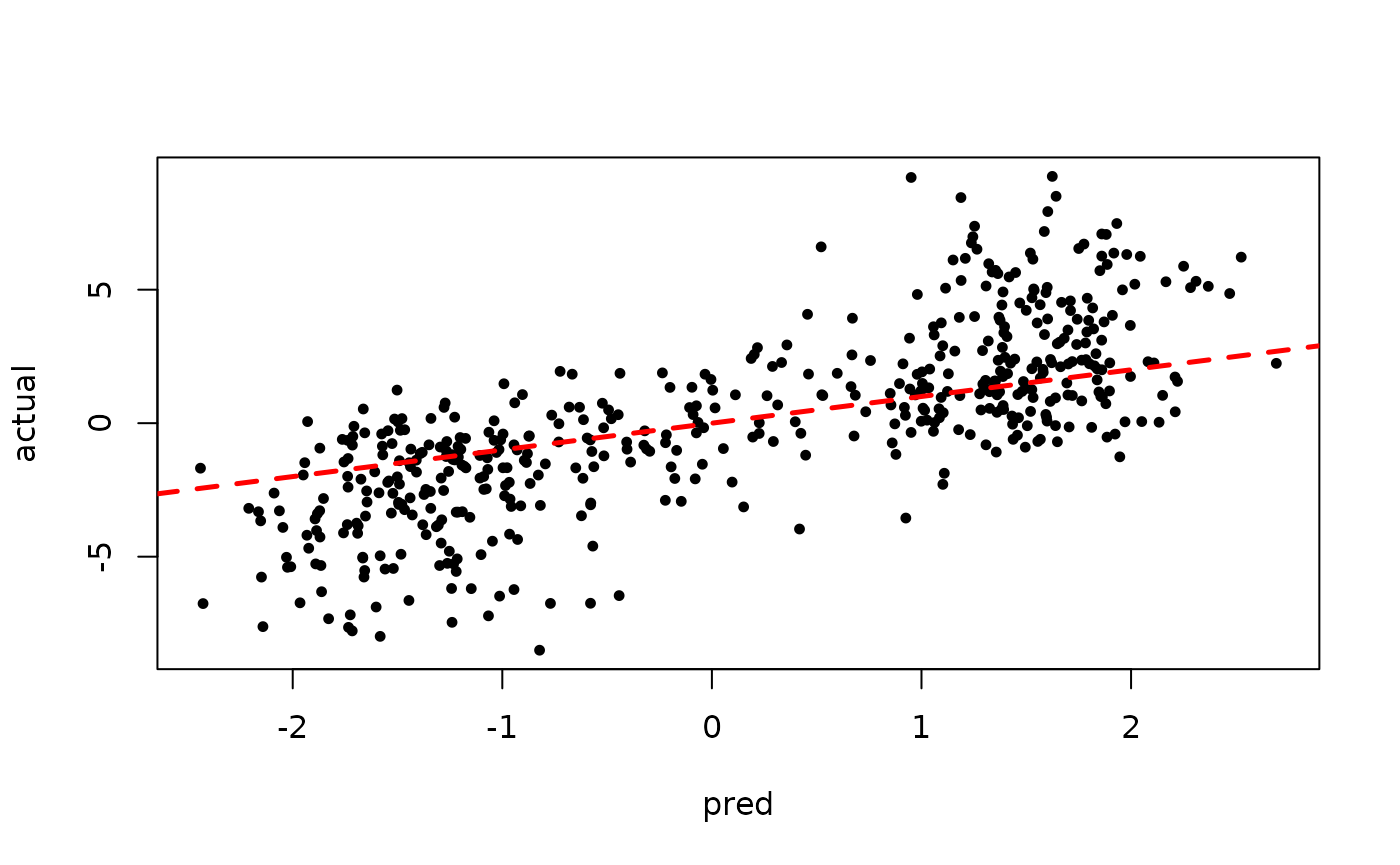

On non-simulated datasets, the first thing we would evaluate is the prediction accuracy.

preds_test <- rowMeans(bart_model_root$y_hat_test) > 0
mean(preds_test == y_test)
#> [1] 0.866

We can also compute the ROC curve for every posterior sample, as well as the ROC of the posterior mean.

num_thresholds <- 1000
thresholds <- seq(0.001,0.999,length.out=num_thresholds)
tpr_mean <- rep(NA, num_thresholds)
fpr_mean <- rep(NA, num_thresholds)
tpr_samples <- matrix(NA, num_thresholds, num_mcmc)
fpr_samples <- matrix(NA, num_thresholds, num_mcmc)
yhat_samples <- bart_model_root$y_hat_test
yhat_mean <- rowMeans(yhat_samples)
for (i in 1:num_thresholds) {
    is_above_threshold_samples <- yhat_samples > qnorm(thresholds[i])
    is_above_threshold_mean <- yhat_mean > qnorm(thresholds[i])
    n_positive <- sum(y_test)
    n_negative <- sum(y_test==0)
    y_above_threshold_mean <- y_test[is_above_threshold_mean]
    tpr_mean[i] <- sum(y_above_threshold_mean)/n_positive
    fpr_mean[i] <- sum(y_above_threshold_mean==0)/n_negative
    for (j in 1:num_mcmc) {
        y_above_threshold <- y_test[is_above_threshold_samples[,j]]
        tpr_samples[i,j] <- sum(y_above_threshold)/n_positive
        fpr_samples[i,j] <- sum(y_above_threshold==0)/n_negative
    }
}

for (i in 1:num_mcmc) {
    if (i == 1) {
        plot(fpr_samples[,i], tpr_samples[,i], type = "line", col = "blue", lwd = 1, lty = 1,
         xlab = "False positive rate", ylab = "True positive rate")
    } else {
        lines(fpr_samples[,i], tpr_samples[,i], col = "blue", lwd = 1, lty = 1)
    }
}
#> Warning in plot.xy(xy, type, ...): plot type 'line' will be truncated to first
#> character
lines(fpr_mean, tpr_mean, col = "black", lwd = 3, lty = 3)

References

Chipman, Hugh A., Edward I. George, and Robert E. McCulloch. 2010. “BART: Bayesian additive regression trees.” The Annals of Applied Statistics 4 (1): 266–98. https://doi.org/10.1214/09-AOAS285.
He, Jingyu, and P Richard Hahn. 2023. “Stochastic Tree Ensembles for Regularized Nonlinear Regression.” Journal of the American Statistical Association 118 (541): 551–70.